Grasshopper ? Podstawy cz. 2 - Projektowanie Parametryczne

Listy danych

W drugim tutorialu zajmiemy się listami danych. Tak jak pisałem w pierwszym poradniku,
jest to bodajże jedna z najważniejszych rzeczy do opanowania w Grasshopperze (często bagatelizowana w innych poradnikach). Komponenty odpowiedzialne za porządkowanie naszych danych, znajdują się w kategorii komponentów “Sets” (o kategoriach pisałem w pierwszym tutorialu).

W jaki sposób Grasshopper porządkuje dane ?

W odróżnieniu od innych programów, Grasshopper daje wgląd w to jak sam działa.
Widzimy w jaki sposób porządkuje dane przed użyciem funkcji, a także jak one wyglądają po jej użyciu. Dzięki temu możemy szybciej dostrzec gdzie w naszym projekcie kryje się błąd. Listy danych porządkowane są wg. adresu w postaci “{A;B;C…}” oraz indeksu danej wartości “(i)”. Każda funkcja (komponent), który modyfikuje w jakiś sposób naszą listę danych, zmienia adresy list poprzez dodanie kolejnej liczby. Dla przykładu mając 10 punktów referencyjnych w komponencie “Pt”, ich adres będzie wyrażony jako “{0}”, kolejność wprowadzenia punktów natomiast będzie stanowiła o ich indeksie “(i)”. Zmodyfikowanie punktów np. poprzez “cull pattern” (usuwanie wg. deseniu) wprowadza nam do adresu kolejną liczbę; adres wygląda teraz tak : “{0,0}” .

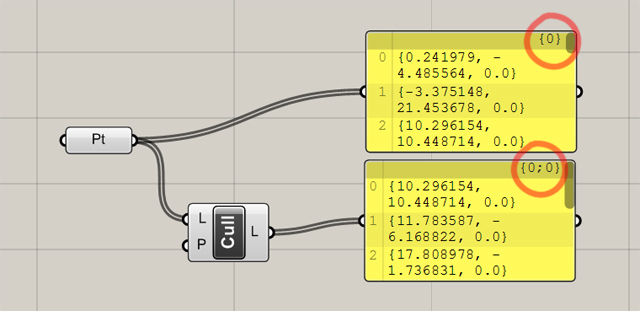
Zmiana długości adresu po zastosowaniu komponentuZarówno w adresie jak i w indeksach, a także w wielu komponentach, wartości liczone są od 0.
Dlatego mając 10 punktów na liście pierwszy będzie miał indeks 0, ostatni 9.

Komponenty w kategorii “Sets”

Kategoria “Sets”

Tak jak pisałem w poprzednim tutorialu, nie będę opisywał każdego komponentu osobno.
W ćwiczeniu 3 nie użyję wszystkich komponentów z kategorii “Sets”, postaram się jednak użyć tych, z których sam najczęściej korzystam i które uważam za najprzydatniejsze. Opiszę za to palety komponentów, dzięki czemu będziemy mieli ogólny pogląd na tą kategorię.

W pierwszej palecie zatytułowanej “List” są komponenty odpowiedzialne za operowanie na całych listach. Z nich korzystamy najczęściej. Mamy tu m.in. takie możliwości jak : odwrócenie listy, wydobycie konkretnej wartości z listy, sprawdzenie długości listy itp.
Następna paleta to “Sequence”. Tutaj mamy także bardzo przydatne komponenty, odpowiedzialne za generowanie najróżniejszych sekwencji liczb, a także za usuwanie wartości z listy wg. różnych deseni.
Trzecia paleta “Strings” zawiera komponenty umożliwiające modyfikowanie samych wartości w listach. Jest to dość drastyczna metoda, używana raczej jako ostateczność. Niemniej jednak czasem bez modyfikowania wartości nie będziemy w stanie wykonać niektórych rzeczy. Poza tym modyfikując wartości bezpośrednio zaoszczędzamy nieraz wiele czasu.
Ostatnia paleta “Tree” to paleta umożliwiająca modyfikowanie całych “drzew” danych. Możemy tutaj np. zamienić kolumny z wierszami (co nie zadziała w przypadku bardziej skomplikowanych list danych, kiedy adres jest wyrażony w więcej niż dwóch liczbach), stworzyć z każdej wartości osobną gałąź poprzez “graft tree”, “spłaszczyć” listę poprzez “flatten tree” (usuwa strukturę drzewa), a także wyczyścić naszą listę z wadliwych wartości dzięki “clean tree”.

Poza komponentami z kategorii “Sets”, przydatnymi w porządkowaniu danych będą też dwa inne z kategorii “Params” -> paleta “Special” :

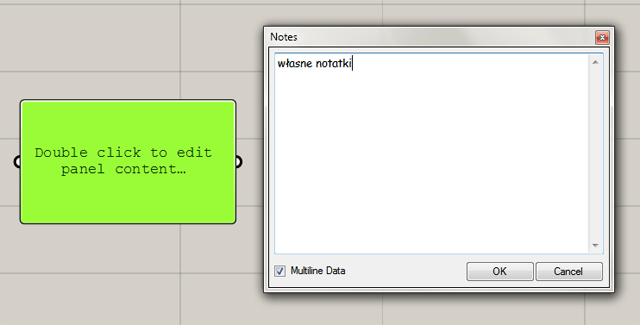
Panel – czyli podgląd danych na wyjściu danego komponentu. Wypisuje on tylko i wyłącznie strukturę danych na wyjściu komponentu. Daje możliwość wyeksportowania wyświetlanej zawartości do m.in. pliku tekstowego. Kiedy nic nie jest połączone do wejścia panelu, można w nim zapisać własne notatki itp. (aby edytować zawartość kliknij na niego lewym dwuklikiem)

Param viewer – Przestawia graficznie strukturę danych w postaci “drzewka” lub rozpisując zawartość podobnie do panelu. Param viewer obrazuje nam całą strukturę danych od początku (na dole “drzewka”) do końca, czyli momentu w którym wstawiamy ten komponent.

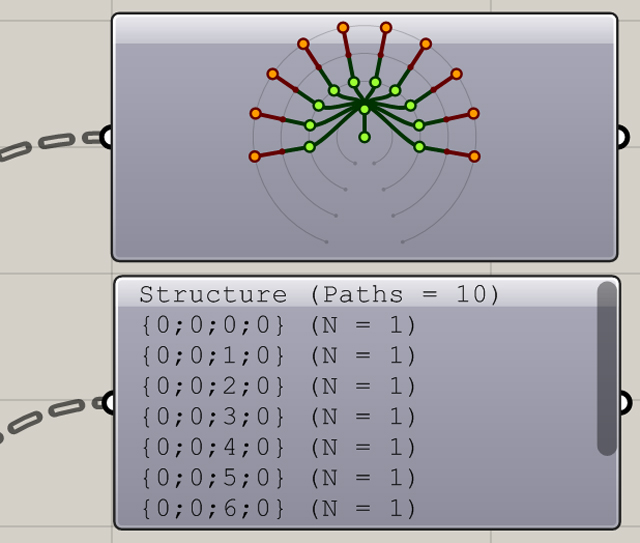
Porządkowanie danych za pomocą komponentów z kategorii “Sets” zaoszczędzi nam wiele nerwów przy konstruowaniu czegokolwiek w GH. Najczęściej problemy w GH zaczynają się od stwierdzenia, że coś co jak myślimy powinno zadziałać, nie działa. Zwykle jest to spowodowane naszym złym pojęciem (przynajmniej moim ;]) o tym jak Grasshopper “widzi” dane. W takim momencie korzystamy z Panel’u bądź też Param viewer’a.Połączenia między komponentami standardowo wyświetlane są na 3 różne sposoby : Jako pojedyncza linia – kiedy mamy jedną wartość w jednej gałęzi, jako podwójna linia – kiedy mamy wiele wartości ale w jednej gałęzi oraz jako linia przerywana, kiedy mamy wiele wartości w wielu gałęziach.

Praktyka

Wstęp do ćwiczenia

     Po tym jak wspomniałem w pierwszym tutorialu o diagramach Voronoi (Woronoja), Przemek
czyli głównodowodzący tej strony wykazał zainteresowanie tym zagadnieniem pod kątem Grasshoppera. Podejrzewam więc, że i Was powinno to zainteresować. O tym czym są diagramy Voronoi, możecie przeczytać w Wikipedii. Tych, których zrazi ścisła, encyklopedyczna definicja, niech przekona fakt, że przyroda “korzysta” z diagramu Woronoja nadzwyczaj często  Wystarczy wspomnieć o umaszczeniu żyrafy, pierzastym użyłkowaniu liścia, kształcie komórek itp. itd. W urbanistyce diagram Voronoi służy czasem do wyznaczenia ścieżek (centra komórek to miejsca które ścieżki mają omijać).
     W tym ćwiczeniu zajmiemy się więc komponentami odpowiedzialnymi za porządkowanie list
danych, na przykładzie formy przestrzennej powstałej dzięki diagramom Voronoi.

Ćwiczenie 3 : Listy danych z wykorzystaniem diagramu Voronoi

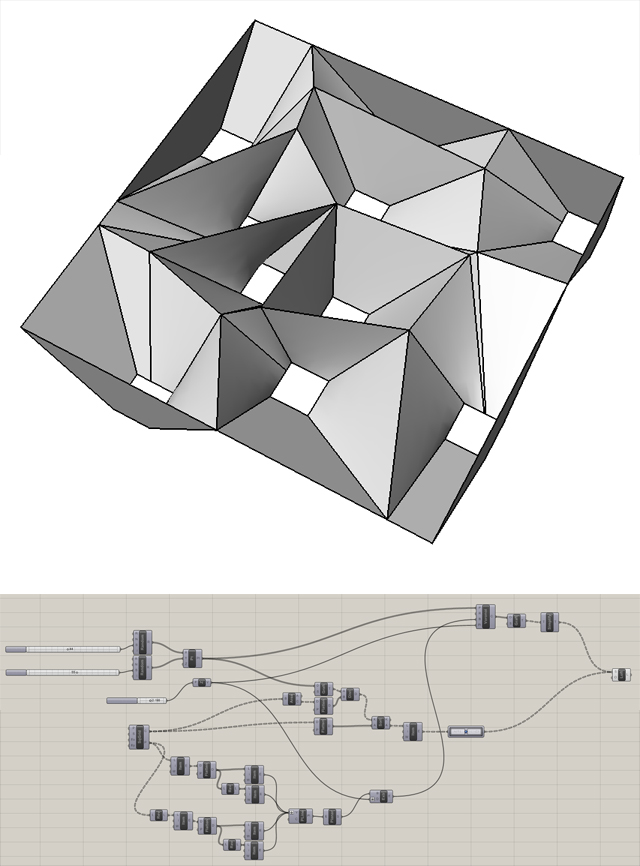
Wynik ćwiczenia 3

Aby skonstruować strukturę widoczną na obrazku należy :

Wykreślić diagram Voronoi dla 10 losowych punktów
Zadać płaszczyznę do kreślenia diagramu
Wygenerować siatkę kwadratową
Wydobyć z siatki kwadratowej cztery jej punkty będące narożnikami całości
Stworzyć prostopadłościan na podstawie tych punktów i zadanej wysokości, dzięki czemu będziemy mogli wskazać w którym miejscu “przycinamy” diagram Voronoi
Znaleźć dla każdej komórki z diagramu Voronoi najbliższą komórkę z siatki kwadratowej
Stworzyć wielościany (funkcja loft) na podstawie par najbliższych sobie komórek

Kreślimy diagram Voronoi dla 10 losowych punktów
Zaczniemy od wygenerowania 10 punktów umieszczonych losowo na płaszczyźnie XY. Aby to zrobić należy umieścić na płótnie komponent “Point XYZ” (kategoria “Vector->paleta “Point”). Daje on możliwość wpływania na położenie punktu poprzez określenie jego współrzędnych. Do wejść X i Y (Z nie jest potrzebne jako, że diagram Voronoi standardowo działa na płaszczyźnie) podpinamy po jednym komponencie “Random” (kategoria “Sets”->paleta “Sequence”).

Komponent ten ma 4 wejścia : R, N, S oraz I :

Range czyli przedział generowanych wartości – klikamy prawym klawiszem na literę R i ustawiamy “set domain” na “0.0 to 10.0″
Number czyli ilość wygenerowanych wartości; pozostawiamy bez zmian (standardowo jest 10, czyli tyle ile potrzebujemy do tego ćwiczenia)
Seed jest odpowiedzialny za “ziarno” losowych wartości. Jeśli ustawimy dla X i Y taką samą wartość S, będziemy mieli punkty rozmieszczone po przekątnej kwadratu, aby tego uniknąć dołączamy po jednym sliderze (kategoria “Params” -> paleta “Special”) do S ustawionym na przedział od 0 do 100, podając dwie różne wartości dla X i Y.
Integer – ogranicza wyniki komponentu do liczb całkowitych; pozostawiamy bez zmian

Powinniśmy otrzymać coś takiego (rozmieszczenie punktów może się różnić) :

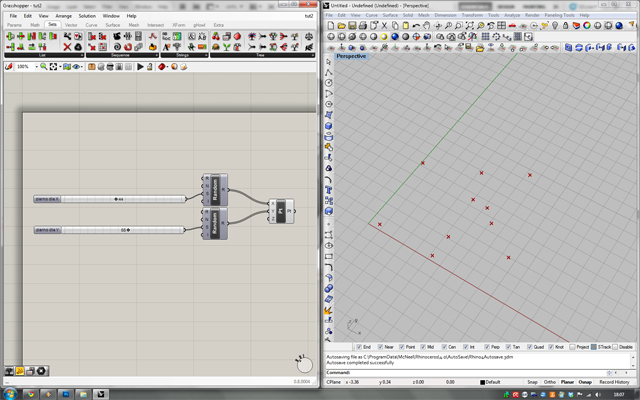
Punkty służące nam do wykreślenia diagramu

Teraz wykreślimy diagram Voronoi dla tych punktów – aby to zrobić skorzystamy z komponentu Voronoi (nie Voronoi Groups). Komponent ten także ma 4 wejścia :

Points – podłączamy tu punkty z komponentu “Point XYZ”
Radius – średnica komórki; zostawiamy bez zmian
Box – obszar w jakim ma być wykreślony diagram; zajmiemy się tym za chwilę
Plane – płaszczyzna na której ma zostać wykreślony diagram; zadamy ją w następnym podpunkcie

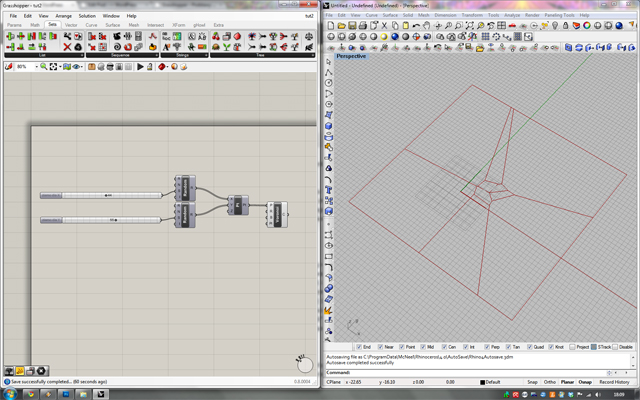
Zadajemy płaszczyznę do wykreślenia Diagramu Voronoi
Wiele komponentów standardowo używa płaszczyzny “World XY” co oznacza, że płaszczyzna ta ma środek w punkcie o współrzędnych (0,0,0) a jej osie OX i OY są takie jak płaszczyzny roboczej w Rhino. Oczywiście diagram Voronoi także korzysta z tej płaszczyzny, co musimy zmienić aby skonstruować naszą strukturę. Znajdujemy więc komponent “Unit Z” generujący wektor o długości równej 1 w osi Z (kategoria “Vector” -> paleta “Vector”). Podłączamy do jego wejścia slider (przyjmijmy dla niego wartości od 0 do 5), a następnie wyjście naszego wektora łączymy z wejściem Pl diagramu. Grasshopper “domyśli” się że chodzi nam o wygenerowanie płaszczyzny o środku w punkcie (0,0, wartość slider’a). Teraz mamy możliwość zmieniania położenia diagramu Voronoi w osi Z o wartość z naszego slidera.

Generujemy siatkę kwadratową
Wyłączmy wpierw wszystkie komponenty które do tej pory stworzyliśmy – robimy to zaznaczając wszystko (ctrl+a), następnie klikając na ikonkę “Disable Preview” na pasku funkcji podstawowych.

Umieszczamy na płótnie komponent “SqGrid” (kategoria “Vector”->paleta “Grid”). Posiada on także cztery wejścia :

Plane – miejsce w którym siatka ma zostać wykreślona; zostawiamy tak jak jest
Size – wielkość oczka siatki; zostawiamy tak jak jest (wartość 1), jako że zadaliśmy przedziały od 0 do 10 przy generowaniu losowych punktów
Ex ilość oczek w osi X; zostawiamy 10 (standardowa wartość)
Ey ilość oczek w osi Y; zostawiamy 10 (standardowa wartość)

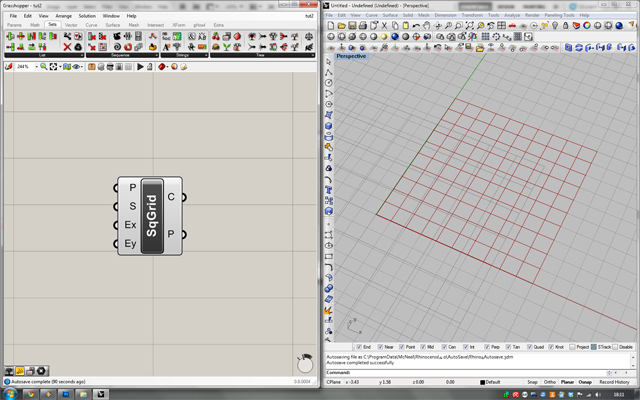
Wydobywamy z siatki jej narożniki
Teraz naprawdę zaczniemy myśleć o tym jak działać z listami danych. W poprzednim podpunkcie stworzyliśmy siatkę kwadratową o stu oczkach. Są one standardowo porządkowane na liście kolumnami – w naszym przypadku jest to 10 kolumn po 10 punktów. W tym wypadku możemy mówić, że indeks odpowiada wierszowi (jak w arkuszu kalkulacyjnym).W tym ćwiczeniu za każdym razem kiedy potrzebne jest użycie funkcji “graft” bądź też “flatten”, umieszczamy na płótnie komponent wykonujący to działanie. Postanowiłem tak robić, aby było czytelne kiedy musimy użyć tych funkcji. W praktyce jednak dużo prościej jest kliknąć prawym klawiszem myszki na wybrane wejście komponentu i znaleźć w opcjach “flatten” lub “graft”.

Na wyjściu P komponentu SqGrid mamy aktualnie 121 punktów – są to narożniki naszych komórek w siatce (jest 11 kolumn po 11 indeksów). Musimy z nich wydobyć pierwszy z pierwszej kolumny punktów, ostatni z pierwszej kolumny, pierwszy z ostatniej kolumny oraz ostatni z ostatniej kolumny.

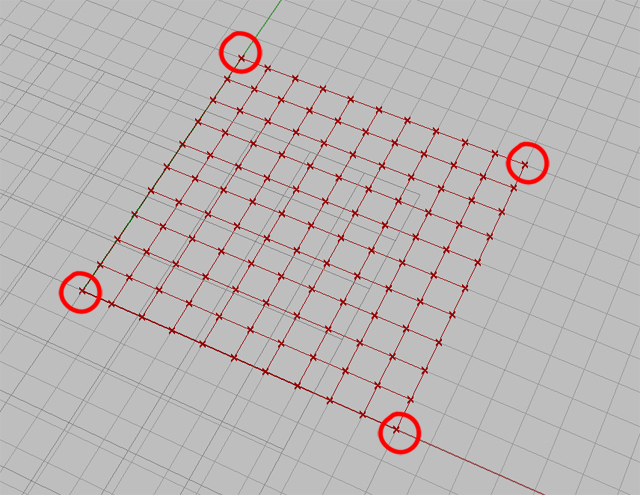
Aby to zrobić umieszczamy na płótnie komponent “List item”(kategoria “Sets”->paleta “List”), połączmy go z wyjściem P w “SqGrid”. Wydobywa on wartości z listy o zadanym indeksie (wejście “i”). W ten sposób wydobyliśmy wszystkie punkty z indeksem (0) – jest ich 11 (11 “gałęzi” po jednym punkcie). Aby wydobyć pierwszy z tych punktów musimy “spłaszczyć” listę poprzez “flatten” (kategoria “Sets”->paleta “Tree”). Otrzymaliśmy w ten sposób jedną “gałąź” z 11 punktami o różnych indeksach. Podłączając teraz do wyjścia “D” w komponencie “flatten” kolejny komponent “List item”, wydobędziemy pierwszy punkt z pierwszej kolumny. Aby było to dobrze widoczne na podglądzie w Rhino, zastosujemy “Disable Preview” do wszystkich komponentów prócz ostatniego “List item” oraz “SqGrid”.

Teraz wydobędziemy ostatni punkt z pierwszej kolumny. Należy pamiętać, że o ile w naszym ćwiczeniu nie mamy zamiaru zmieniać ilości oczek w siatce kwadratowej, o tyle w praktyce często będziemy chcieli mieć taką możliwość. Dlatego nie możemy podłączyć “List item” z indeksem ustawionym na 10, celem wydobycia jedenastego punktu pierwszej kolumny. Aby Grasshopper zawsze wydobywał ostatnią wartość z listy, należy odwrócić listę (tą z której mamy pierwszy punkt w pierwszej kolumnie) poprzez zastosowanie komponentu “Reverse list” (kategoria “Sets”->paleta “List”), następnie wstawić kolejny komponent “List item”. Dzięki temu Grasshopper zawsze będzie wydobywał ostatnią wartość z listy, niezależnie od jej długości; właśnie otrzymaliśmy ostatni punkt z pierwszej kolumny.

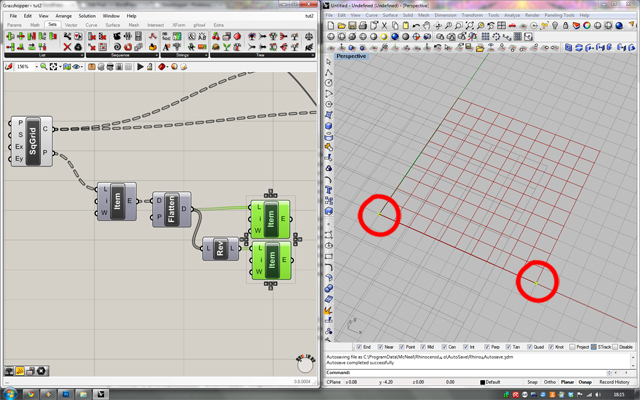
Aby wydobyć pierwszy i ostatni punkt z ostatniej kolumny musimy wpierw odwrócić naszą listę z wyjścia P komponentu SqGrid, następnie skopiować i wkleić komponenty dotychczas użyte do wydobycia pierwszego i ostatniego punktu z pierwszej kolumny. Ostatecznie łączymy pierwszy komponent “List item” z wyjściem “Reverse list”. W ten sposób otrzymaliśmy pozostałe dwa potrzebne punkty.

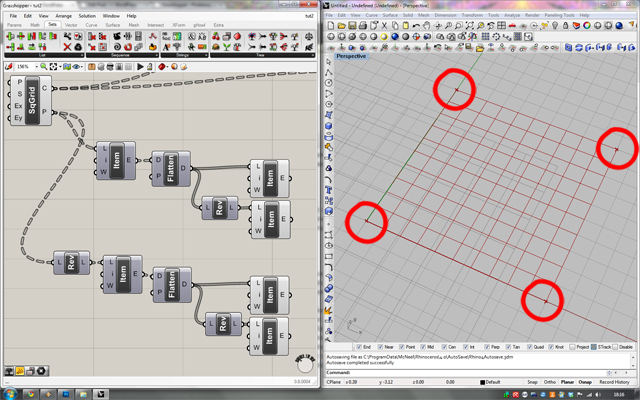
Tworzymy prostopadłościan “przycinający” diagram Voronoi
Przed przystąpieniem do tego podpunktu wyłączmy podgląd wszystkich komponentów, prócz tych wydobywających nasze cztery punkty i kreślącego diagram Voronoi.

Jedno z wejść komponentu “Voronoi”, konkretnie Box, ma za zadanie ograniczenie powierzchni na jakiej ten diagram jest kreślony. Aby stworzyć prostopadłościan do tego potrzebny umieszczamy na płótnie komponent “Polyline” (polilinia; kategoria “Curve”->paleta “Spline). Klikamy na jego wejście Close prawym klawiszem myszy i ustawiamy “Set boolean” na wartość “True”. Następnie w odpowiedniej kolejności połączamy punkty w narożnikach siatki z wejściem V polilinii (aby podłączyć więcej niż jeden komponent z wejściem trzymaj wciśnięty klawisz shift). Znajdujemy komponent “Planar srf” (kategoria “Surface”->paleta “Freeform”), i łączymy go z wyjściem “Pline”. Uzyskaliśmy właśnie podstawę prostopadłościanu. Jeśli widzisz przekątne podstawy, oznacza to że w złej kolejności podłączyłeś punkty – zmień to .

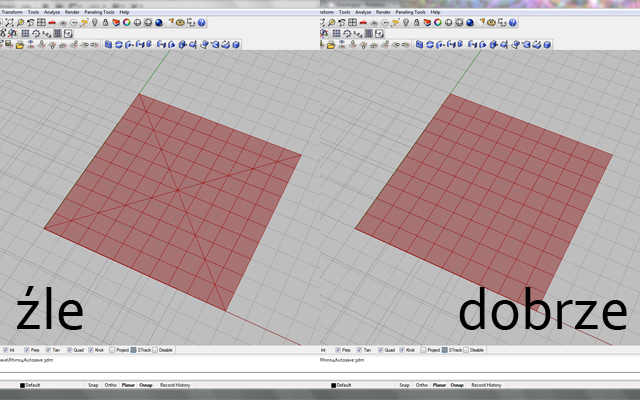
Znajdujemy komponent “Extrude” (kategoria “Surface”->paleta “Freeform”) i umieszczamy go na płótnie. Do wejścia B komponentu przyłączamy wyjście z komponentu “Planar srf”. Do wejścia Direction podłączamy wyjście wektora z podpunktu “Zadajemy płaszczyznę do wykreślenia Diagramu Voronoi”. Określa on teraz wysokość naszego prostopadłościanu, która jest równa wysokości na jakiej znajduje się diagram. Gdybyśmy teraz zastosowali ten prostopadłościan do ograniczenia diagramu, moglibyśmy się spodziewać że albo nic nie zobaczymy, albo diagram będzie błędnie ograniczany. Dlatego musimy sprawić aby prostopadłościan był wyższy – robimy to mnożąc wektor razy 2. Klikamy więc na wejście D “Extrude” i w polu “Expression” wpisujemy “d*2″ (bez cudzysłowia). Podłączamy wyjście “Extrude” do wejścia B “Voronoi”.

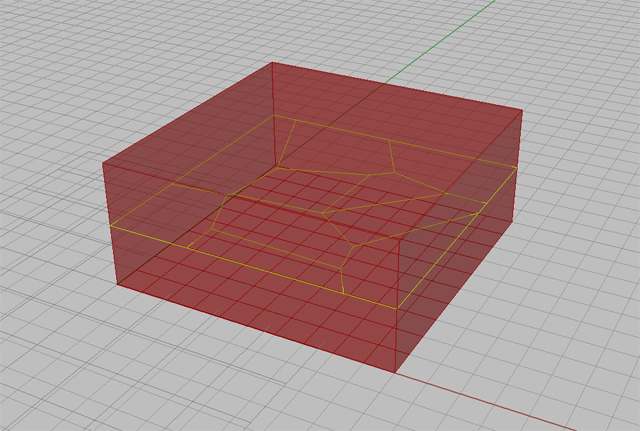
Spędzasz dużo czasu przed komputerem? Zadbaj o swój komfort i wygodę! Sprawdź: Biurko komputerowe

Znajdujemy najbliższe oczka siatki
Aby znaleźć najbliższe komórce oczko siatki obliczymy dystans każdego centrum komórki do centrum każdego oczka. Centra naszego diagramu Voronoi już mamy(to punkty wykreślające diagram), pozostaje znaleźć centra oczek w siatce. Używamy do tego komponentu “Area” (kategoria “Surface”->paleta “Analysis”). Komponent ten pokazuje zarówno powierzchnię obiektu jak i jego centroid. Łączymy go z wyjściem C “SqGrid” – otrzymaliśmy 100 punktów (10 kolumn po 10 indeksów). Teraz na płótnie umieszczamy “Distance” (kategoria “Vector”->paleta “Point”). Gdybyśmy w tym momencie połączyli wyjście “Pt” (punkty Voronoi) do wejścia A, natomiast 100 centroid do wejścia B otrzymalibyśmy tylko 100 wyników ponieważ dystans byłby obliczany tylko dla pierwszej kolumny punktów z siatki kwadratowej (ponieważ punkty z diagramu są tylko w jednej kolumnie, a punkty z siatki w 10 kolumnach).

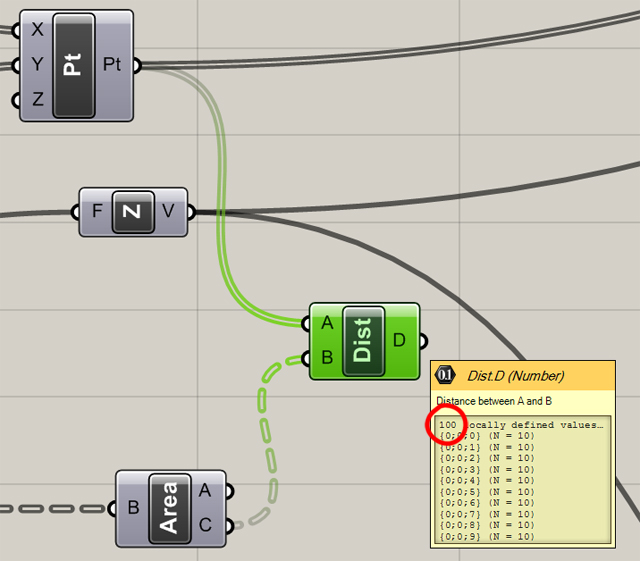
Złe porządkowanie danych nie daje wymaganych wartości

Musimy więc użyć “graft” (kategoria “Sets”->paleta “Tree”) na wyjściu punktów z “Pt”. Utworzymy w ten sposób 10 kolumn po jednym punkcie. Aby porównać każdy z tych 10 punktów z każdym ze 100 punktów z siatki użyjemy jeszcze komponentu “flatten” na wyjściu naszych centroid (inaczej porównalibyśmy każdy punkt z “Pt” z odpowiadającą mu kolumną z siatki). Dopiero teraz łączymy wyjścia z “graft” i “flatten” do wejść A i B “Dist”.

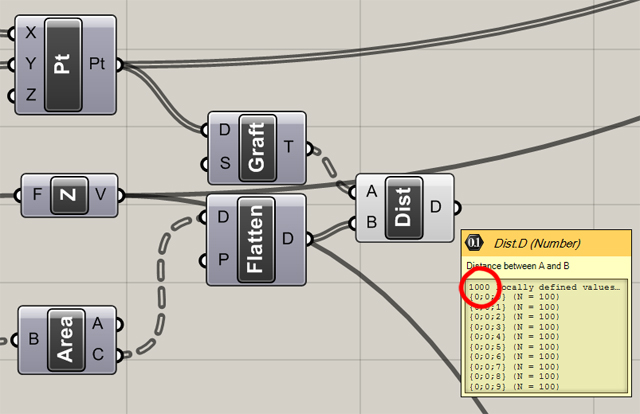
Prawidłowe uporządkowanie struktury danych

Aby wydobyć oczka siatki najbliższe odpowiadającym im komórkom z diagramu, użyjemy “Sort list” (kategoria “Sets”->paleta “List”). Porządkuje on wartości w każdej kolumnie rosnąco. Do wejścia K podłączamy wyjście z “Dist”. Wejście A natomiast służy do sortowania synchronicznie innej listy na podstawie wyniku sortowania z wejścia K. Podłączamy do A wyjście C z “SqGrid”, po drodze oczywiście stawiając “flatten” (aby naśladować “flatten” użyty do centroid).

Na wyjściu A mamy teraz oczka siatki posortowane wg. odległości do każdego z punktów diagramu. Wydobywamy tylko pierwsze oczko z każdej kolumny (tylko najbliższe) używając “List item”. Jeśli zrobiłeś/aś wszystko prawidłowo, oczka na wyjściu “List item” powinny być posortowane w 10 kolumnach po 1 indeksie (1 oczku). Adres każdej kolumny powinien wyglądać tak : {0;0;0-9;0}.

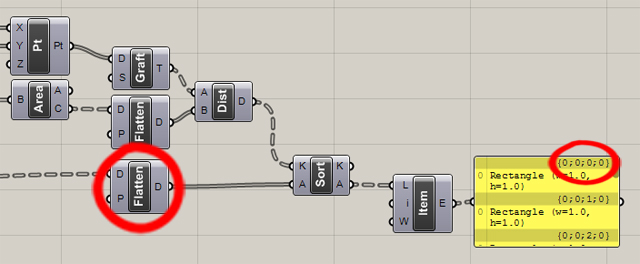
Zastosowanie “flatten” porządkuje oczka siatki w ten sam sposób jak obliczone odległości

Ostatnim krokiem będzie :

Tworzenie wielościanów (funkcja loft) na podstawie par najbliższych sobie komórek
Zanim przystąpimy do użycia “Loft” niezbędnym będzie użycie “graft” na wyjściu z “Voronoi” (aby każda komórka miała własną kolumnę). Po “graft” wstawiamy także “Simplify tree” (kategoria “Sets”->paleta “Tree”), co zmieni adresy komórek z {0;0;0;n} na {n}.

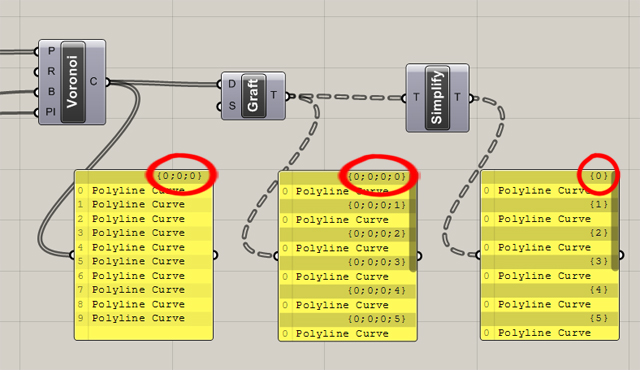
Kolejne etapy odpowiedniego adresowaniaKomponent “Simplify tree” usuwa zbędne (nieprzyjmujące innych wartości niż 0) liczby w adresach kolumn. Robi to jednak tylko z liczbami znajdującymi się przed pierwszym istotnym miejscem w adresie ( X;X;{3} ) – kolejne liczby nie są usuwane, niezależnie od ich istotności ( X;X;{3;0} )

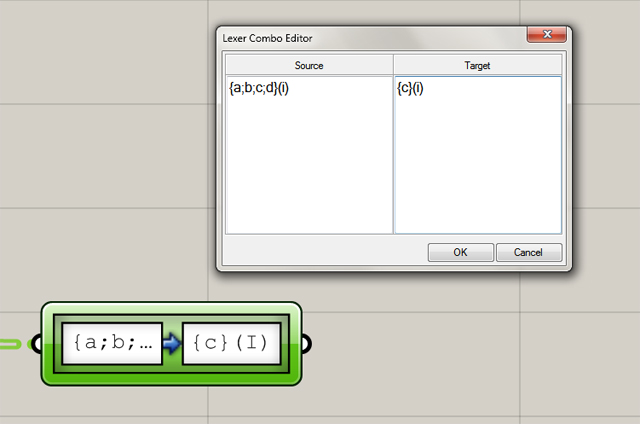
Komponent “Loft” w Grasshopperze nie jest w stanie połączyć ze sobą dwóch krzywych kiedy ich kolumny mają adresy różniące się ilością znaków, np. {0,1} z {0,0,1} lub {1}. Dlatego należy sformatować adresy naszych oczek z {0;0;0-9;0} do {0-9}. Do tego celu nie możemy użyć “Simplify tree” (patrz ramka), poradzimy sobie z tym używając “Path mapper” (kategoria “Sets”->paleta “Tree”). “Path mapper” daje nam możliwość dowolnego edytowania adresów, co często jest jedyną możliwością działania. Uruchamiamy ten komponent za pomocą lewego dwukliku. W lewym okienku wpisujemy “{a;b;c;d}(i)” w prawym natomiast “{c}(i)”. Dzięki temu usunęliśmy wszystkie zbędne liczby z adresu oraz sformatowaliśmy adres oczek z siatki do tej samej postaci w jakiej jest adres komórek z “Voronoi” po uprzednich zabiegach.

Łączymy wyjścia “Path mappera” i “Simplify tree” z “Loft” (kategoria “Surface”->paleta “Freeform”). Kolejność połączenia oczywiście ma wpływ na to co otrzymamy, jest to w tym przypadku związane z działaniem samego “Loft”. Najpierw podłączamy krzywe z “Voronoi”, później oczka z siatki.

Aby “Loft” zadziałał w tym wypadku lepiej, kliknij prawym klawiszem na jego wejście O i zaznacz w “Loft options” opcję “Align sections”. Jeśli to czytasz, to najprawdopodobniej masz teraz na ekranie strukturę przypominającą tę :

Jeśli planujesz budowę domu i potrzebujesz profesjonalnej pomocy, rekomendujemy biuro architektoniczne Poznań.

Podsumowanie

Tak jak ostatnio czekam na Wasze komentarze, sugestie i życzenia. Jeśli przebrnęliście przez całe to ćwiczenie, i rozumiecie jak działa każdy opisany tu komponent, możecie na chwilę unieść się dumą;). Próbujcie także eksperymentować – może uda się komuś za pomocą sliderów generować dowolną ilość punktów w diagramie Voronoi(banalne), albo generować całą strukturę na siatce kwadratowej o różnej ilości oczek w X i Y (trudniejsze)?

Jesteś elektrykiem, spawaczem, hydraulikiem, monterem? Sprawdź – oferty pracy za granicą.