Pierwszą część poradnika dla średnio zaawansowanych poświęcam atraktorom. Znajomość podstaw jest wymagana, stosuję w tym ćwiczeniu wiele skrótów myślowych.

Dlaczego atraktory ?

     Pomijając swoją skomplikowaną definicję encyklopedyczną, atraktory są bardzo łatwym zagadnieniem dla “adeptów” Grasshopper’a. Rządzą się bardzo prostym prawem – “im bliżej tym… im dalej tym… “. W ćwiczeniu nie będzie nawet “zabawy” z listami danych – w tej kwestii użyjemy bardzo prostych komponentów. Mimo to na forum Grasshopper’a pojawiają się jednak co jakiś czas pytania o atraktory, w szczególności o to jak użyć większej ilości punktów “atrakcyjnych”  . W naszym ćwiczeniu będziemy mogli zastosować dowolną ilość atraktorów.

Atraktory w naturze

     Jeśli przeczytaliście artykuł na wikipedii o atraktorach, możecie mieć do nich mieszane uczucia. Gdybym jednak czytał definicje matematyczne wszystkiego co można znaleźć w Grasshopperze, to nigdy bym go nawet nie uruchomił na swoim komputerze.

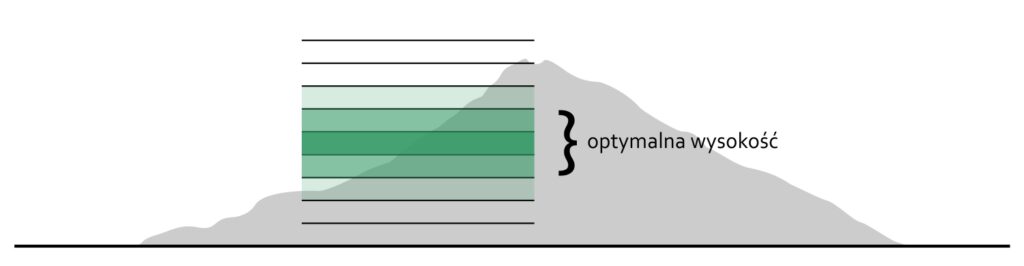
     W przyrodzie atraktorem może być np. wysokość nad poziomem morza – rośliny potrzebują odpowiednich warunków, które są dostępne tylko na danej wysokości (nasłonecznienie, ilość tlenu, podłoże itp.). W ten sposób możemy zaobserwować gradient częstości występowania danego gatunku względem wysokości.

Ćwiczenie

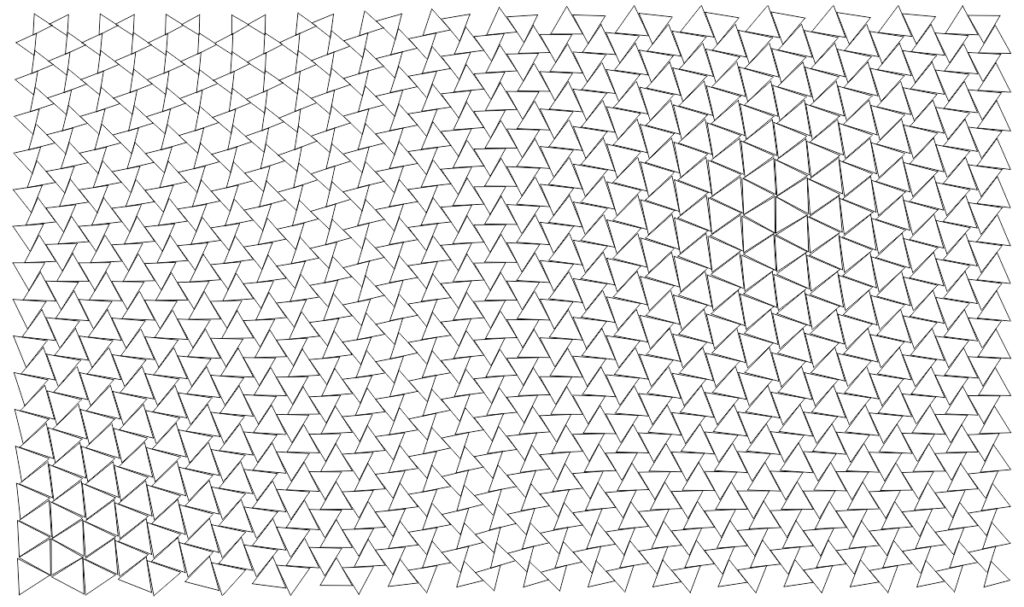
  Zastanówmy się więc – na czym polega logika tej geometrii? Zanim zaczniemy układać algorytm, musimy jasno sprecyzować czego od niego oczekujemy. Mój atraktor działa na siatkę trójkątną (Triangular grid), obracając i przeskalowując trójkąty siatki w stopniu zależnym od odległości do punktu atraktora. Atraktorów może być wiele (to oznacza, że nie może być maksymalnej liczby możliwych atraktorów).

Po takim naszkicowaniu logiki naszego algorytmu, przystępujemy do działania.

Poszukujesz mebli, aby urządzić swoje biuro? Meble biurowe Poznań – ergonomia i design w jednym! 

Plan działania…

…wygląda następująco :

1. Tworzymy siatkę trójkątną
2. Określamy punkty atraktora
3. “Filtrujemy” odległości, tak aby przejścia pomiędzy atraktorami były płynne
4. Konwertujemy dane tak aby mieć pełną kontrolę nad kątami obrotu i stopniem powiększenia zadanych trójkątów.
5. Nadajemy maksymalny kąt o jaki mogą się obrócić trójkąty
6. “Odwracamy” wartości kątów, celem wykorzystania ich do skalowania
7. Po skalowaniu offsetujemy trójkąty, tak aby na siebie nie zachodziły

Tworzymy siatkę trójkątną; określamy punkty atraktora

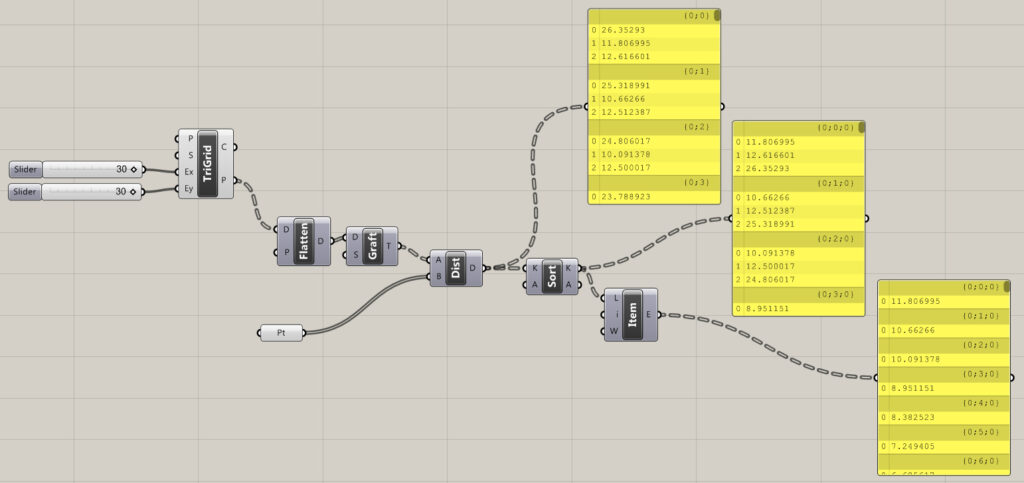
  Aby prawidłowo “przefiltrować” dane odległości, musimy wybrać te najkrótsze, tj. mając trzy atraktory, każda komórka siatki ma możliwość przejęcia tylko jednej z trzech odległości – w naszym przypadku najkrótszej. Dlatego musimy porównać odległości w trójkach – najpierw komórki siatki przechodzą przez “flatten” (usuwamy wszelkie dane na temat adresu komórki), później stosujemy “graft” tak aby każda komórka miała swoją “gałąź” w “drzewie danych”. Teraz umieszczamy komponent “Distance” na płótnie – do wejścia “A” podłączamy nasze komórki, do “B” natomiast punkty atraktora. Gdybyśmy nie zastosowali “graft” na komórach siatki, komponent “Distance” porównałby dane zgadzające się indeksami (indeksy 1, 2, 3), następne indeksy siatki byłyby porównywane z ostatnim atraktorem.
(Patrz tutorial “Podstawy cz.1″; “longest list”)

Konwertujemy dane tak aby mieć pełną kontrolę nad kątami obrotu i stopniem powiększenia zadanych trójkątów.

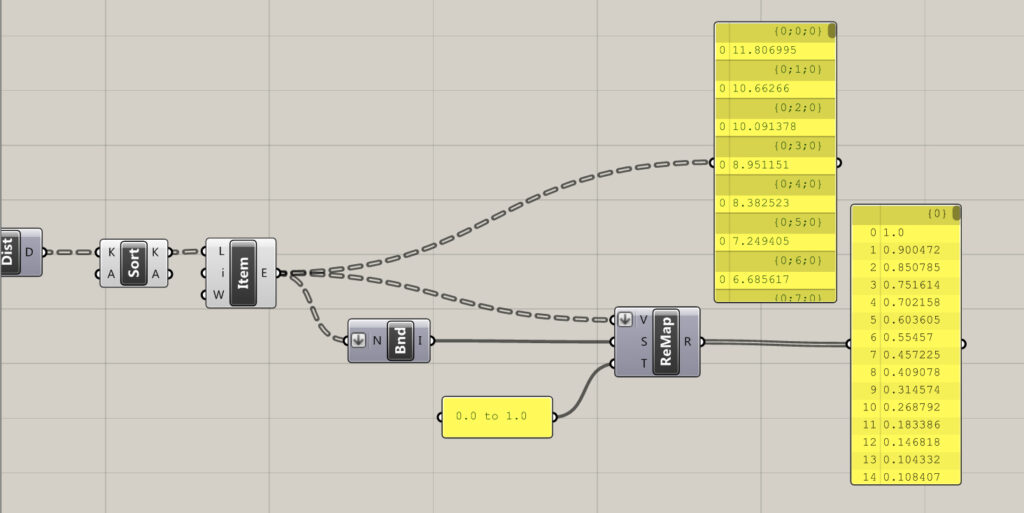
  Odległości jakie otrzymaliśmy po ich porównywaniu, mogą przyjmować najróżniejsze wartości. Często można się spotkać z tym, że ktoś do dalszej pracy zmienia je poprzez mnożenie, dodawanie, odejmowanie itp. To jednak nie daje nigdy pełnej kontroli nad wartościami, dlatego powinniśmy je przekonwertować na wartości mieszczące się w zadanym przedziale (można sobie wyobrazić “przeskalowanie” wartości do odpowiadającego “wymiaru”). Użyjemy zatem komponentu “Remap values”. Posiada on trzy wejścia : wartości “V”, źródłowy przedział liczbowy “S” oraz przedział liczbowy docelowy “T”. Do V podłączamy nasze “przefiltrowane” wartości. Użyjemy na nich także komponentu “Bounds”, aby stworzyć z nich przedział liczbowy “Domain” – podłączamy go do wejścia “S”. Ostatnim krokiem jest zadanie przedziału w którym mają się mieścić nowe wartości, standardowo jest to od 0 do 1 – i tyle zostawiamy. (“Flatten” na wejściu “V” został użyty celem dalszej “obróbki”)

Nadajemy maksymalny kąt o jaki mogą się obrócić trójkąty

     Dzięki temu, że przekonwertowaliśmy zbiór wartości na zbiór mieszczący się w przedziale od 0 do 1, mamy teraz pełną kontrolę nad kątem obrotu trójkątów. Domyślnie kąt obrotu w Grasshopperze podawany jest w radianach – dlatego żeby określić maksymalny kąt obrotu użyjemy liczby pi (kategoria “Math”). Jako że operujemy na trójkątach, maksymalny kąt obrotu ustalamy na pi/3 (60 stopni). Mnożymy pi/3 razy nasze wartości. Umieszczamy komponent “Rotate” na płótnie, do wejścia “G” podczepiamy wyjście “C” z “Triangular grid”; do wejścia “A” nasze wartości po pomnożeniu przez pi/3; do wejścia “P” zadajemy punkty z wyjścia “P” komponentu “Triangular grid” (środki trójkątów). Wszystkie wejścia muszą wcześniej zostać ustawione na “flatten”, inaczej adresy obiektów i wartości nie będą sobie odpowiadać. Po podłączeniu wszystkiego, możemy spojrzeć na okno Rhinocerosa – widzimy już obrócone trójkąty.

Jeśli planujesz budowę domu i potrzebujesz profesjonalnej pomocy, rekomendujemy biuro architektoniczne Poznań.

Na zakończenie

     To już koniec poradnika na temat atraktorów. Jeśli ktoś uzna, że naprawdę rozumie “jak to te atraktory działają” można się pokusić o spróbowanie utworzenia atraktora w postaci krzywej, lub nawet bryły (jest to naprawdę proste).
     Następna część poradnika będzie o strukturach waflowanych (bardzo kiepskie tłumaczenie  ). Jak zwykle czekam na komentarze i przede wszystkim pytania.

Jeśli szukasz partnera, który zajmie się generalnym wykonawstwem inwestycji budowlanej, Workdei jest najlepszym wyborem.