W kolejnej lekcji języka programowania Processing (poprzednia jest tutaj), zajmiemy się krzywymi Beziera. Dlaczego ? Ponieważ krzywe te są bardzo często podstawowym środkiem definiowania nie-liniowej geometrii np. fasad lub dachów. Nie są one co prawda tak popularne jak krzywe B-Spline (chociaż są ich najprostszą wersją), lub ich rozszerzona wersja – NURBS, ale od nich wszystko się zaczęło, więc warto przyjrzeć się im z bliska (są na przykład używane w programie Adobe Illustrator).
Na początek omówimy podstawy tworzenia krzywych, i kilka technicznych elementów pomocnych w kreowaniu trójwymiarowych struktur w Processing. Potem stworzymy program rysujący powierzchnię dachu (jak powyżej) i eksportujący ją do pliku.
Przed Tobą budowa domu? Postaw na pomoc specjalistów z Milwicz Architekci. Zdecyduj czy chcesz skorzystać z gotowego projektu czy może marzy Ci się indywidualny projekt domu?
————————————————————–
Spróbujmy napisać kilka lini kodu rysujących przykładową krzywą Beziera. Aby to zrobić potrzebujemy czterech punktów – początku, czyli tzw. pierwszego punktu zakotwiczenia, dwóch punktów kontrolnych, i drugiego punktu zakotwiczenia, czyli końca krzywej.
Zdefiniujmy zatem łańcuch współrzędnych: cztery współrzędne X (łańcuch będzie miał nazwę ‘px’), i cztery współrzędne Y (łańcuch o nazwie ‘py’)
float px [] = new float[4];
float py [] = new float[4];
w ten sposób zdeklarowaliśmy oba łańcuchy, które są teraz gotowe do użycia. Każdy z nich ma cztery pozycje, w których będzie trzymał jedną współrzędną. Przypiszmy im zatem teraz wartości – współrzędne punktów kontrolnych i skrajnych dla krzywej, w układzie współrzędnych XY (liczonym od lewego górnego rogu okna).
px[0] = 50; py[0] = 50; //pierwszy punkt kontrolny – początek krzywej
px[1] = 40; py[1] = 170; //drugi punkt kontrolny
px[2] = 270; py[2] = 170; //trzeci
px[3] = 250; py[3] = 250; //czwarty – koniec krzywej
size(300,300); //otwórzmy okno o rozmiarach 300 x 300 pikseli
noFill(); //wyłączmy wypełnianie obiektów (o tym później)
bezier(px[0],py[0], px[1],py[1], px[2],py[2], px[3],py[3]); //i narysujmy krzywą
Po wpisaniu powyższego kodu do edytora i naciśnięciu przycisku start, powinniśmy zobaczyć poniższy obraz :
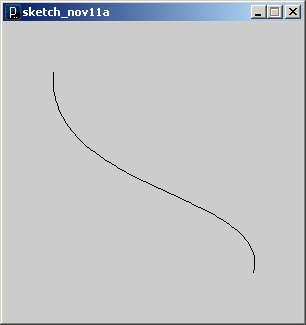
Wygląda ciekawie, ale nadal trochę tajemniczo.. Żeby zrozumieć lepiej, jak działają krzywe beziera, narysujmy punkty kontrolne. Dodajmy na końcu poniższe linie :
fill(255,0,0); //zmieniamy kolor na czerwony (podając kolejno wartości r, g, b)
ellipse(px[0], py[0] ,8,8); //punkt nr 1
ellipse(px[1], py[1] ,8,8); //punkt nr 2
ellipse(px[2], py[2] ,8,8); //punkt nr 3
ellipse(px[3], py[3] ,8,8); //punkt nr 4
a żeby zobaczyć jak wygląda tak zwany ‘control polygon’, połączmy je liniami:
stroke(50,100); //ustawiamy kolor i przezroczystość linii
line(px[0], py[0] ,px[1], py[1]);
line(px[1], py[1] ,px[2], py[2]);
line(px[2], py[2] ,px[3], py[3]);
Po dodaniu powyższych linii, uruchamiamy szkic (przyciskiem run, albo ctrl+R) i widzimy krzywą jak poniżej :
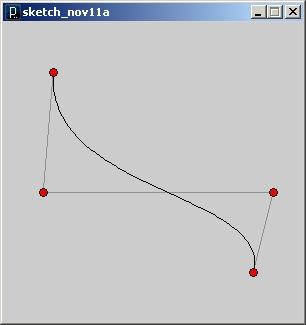
Patrząc na ten przykład, można łatwo zauważyć podstawową właściwość krzywej Beziera : początek i koniec są styczne do linii kontrolnych, a to można sprytnie wykorzystać przy tworzeniu bardziej skomplikowanych geometrii.
Spróbujmy teraz zrobić z tego coś ciekawszego, czyli wykorzystać replikację (poprzez użycie pętli FOR – więcej informacji o tym jak jej używać jest w poprzednim tutorialu). Generalnie najciekawsze efekty daje niewielka modyfikacja współrzędnych punktów kontrolnych, i narysowanie wszystkich tak powstałych krzywych razem obok siebie. Dodajmy zatem :
noFill(); //wyłączamy wypełnianie
for (int i=0;i<20;i++) //uruchamiamy pętlę na 20 powtórzeń
{
px[0] = px[0]+5; //przesuwamy punkt 0 w prawo
py[1] = py[1]+8; // punkt 1 w dół
py[2] = py[2]-4; //punkt 2 w górę
px[3] = px[3]+2; //punkt 3 lekko w prawo
bezier(px[0],py[0], px[1],py[1], px[2],py[2], px[3],py[3]); //i rysujemy krzywą
}
Spędzasz dużo czasu przed komputerem? Zadbaj o swój komfort i wygodę! Sprawdź: Biurko komputerowe
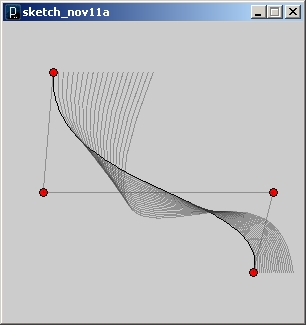
Ciekawą wizualizację krzywych razem z liniami kontrolnymi można uzyskać przenosząc dwie linijki kodu:
for (int i=0;i<20;i++)
{
nad linię z komendą fill(255,0,0); , ponieważ wtedy w pętli znajdzie się procedura rysowania linii i czerwonych kółek. Otrzymamy wtedy obraz pokazujący dokładnie ‘wędrówkę’ punktów kontrolnych :
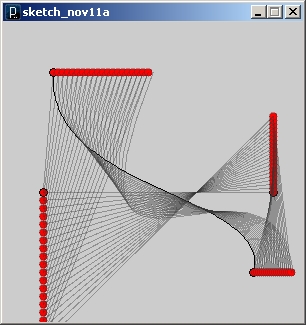
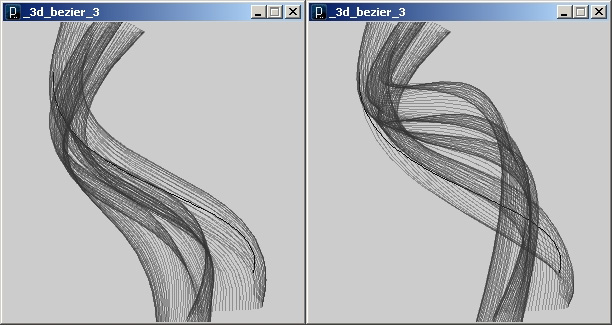
Pewnie ktoś z czytelników zapyta.. ‘ok, wporządku, ale do czego można tego teraz użyć’ ? Otóż w parametrycznym modelowaniu często spotykamy się z modelowaniem jakiejś powierzchni (np dachu) przez przeciągnięcie jednego profilu wzdłuż krzywej (tzw. szyny – ‘sweep profile along rail curve’ ), lub zbudowanie z wszystkich krzywych jednej powierzchni (‘loft curves’). Tak też spróbujemy zrobić za kilka chwil.
——————————————————————————-
Najpierw jednak, aby ułatwić nam nieco modelowanie trójwymiarowych obiektów, i ich przestrzenną ocenę, musimy dodać do programu element interaktywny. Inaczej będziemy ciągle w dwuwymiarowym, statycznym świecie. Ta mała dygresja jest raczej konieczna do tego, żeby przejść do kolejnego, bardziej ekscytującego (!) etapu programowania w trzech wymiarach.
W Processing możemy pisać programy na dwa sposoby : liniowy, gdzie zwyczajnie wpisujemy komendy jedna po drugiej, np :
size(300,300,P3D); //ustawiamy okno
translate(150,150); //przesuwamy układ współrzędnych na środek ekranu (połowa szerokości, połowa wysokości)
rotateX(PI/3); //obracamy układ współrzędnych wokół osi X
rotateZ(PI*1.7); //i wokół osi Y
box(50); //i rysujemy sześcian
W ten sposób program wykonuje wszystkie polecenia po kolei, i zatrzymuje się na końcu. Możemy w międzyczasie wykonywać pętle, definiować wiele graficznych elementów i pisać nieskończone ilości instrukcji – ale wszystko zostanie wykonane tylko raz.
Drugi sposób, to sposób nieliniowy, interaktywny i zorientowany zdarzeniowo. To znaczy, że po uruchomieniu programu, instrukcje będą wykonywane w niekończącej się pętli (ok 20-30 razy na sekundę), a program może w tym czasie rysować dowolne rzeczy, wydawać dźwięki, odgrywać video, i co najważniejsze reagować na zdarzenia. Takimi zdarzeniami zazwyczaj są manipulacje myszką i naciskanie klawiszy na klawiaturze, ale może to też być bardziej skomplikowany bodziec, jak na przykład obraz z kamery video, lub dźwięk z mikrofonu.
Program taki wygląda tak:
void setup()
{
println(“ta instrukcja wykona się 1 raz”);
}
void draw()
{
println(“ta instrukcja wykona się wiele razy”);
}
Czyli ma dwie części : setup, i draw. Pierwsza wykonuje się tylko raz, dokonujemy w niej ustawienia okna, początkowych zmiennych, ładujemy czcionki, obrazy i dźwięki. Druga (draw) to część która będzie wykonywać się w nieskończoność, dopóki nie zakończymy programu.
Ten sam program, w wersji interaktywnej będzie wyglądał tak :
void setup()
{
size(300,300,P3D); //ustawiamy okno (włączamy też tryb pracy w trzech wymiarach)
}
void draw()
{
background(160); //czyścimy tło przed narysowaniem czegokolwiek
translate(150,150); //przesuwamy układ współrzędnych na środek ekranu (połowa szerokości, połowa wysokości)
rotateX(mouseY*PI/300); //obracamy układ współrzędnych wokół osi X (wykorzystujemy pozycję myszki!)
rotateZ(mouseX*PI/300); //i wokół osi Y
box(50); //i rysujemy kostkę
}
Po uruchomieniu powyższego kodu, zobaczymy radośnie obracający się sześcian
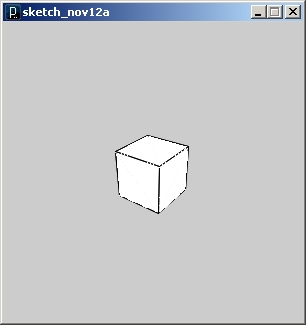
Po tej małej dygresji zacznijmy więc nowy szkic (wybierając z menu File >> New). Na początek, tak jak poprzednio, deklarujemy współrzędnych punktów kontrolnych
float px [] = new float[4];
float py [] = new float[4];
I przejdźmy do trybu 3D – robi się to poprzez deklarację size(szerokość, wysokość, tryb). Tryb może być wyrażony przez P3D – standardowy silnik Javy (działa w oknie przeglądarki stron www), albo przez OPENGL – szybszy i dużo lepszy graficznie silnik, ale działający tylko w oknie Processingu albo po skompilowaniu szkicu do pliku .exe.
void setup()
{
size(600,400,P3D); //tworzymy okno (tym razem trochę większe!)
}
i zaczynamy część ‘dynamiczną’
void draw()
{
background(160); //czyścimy tło
translate(300,200);//przesuwamy układ współrzędnych na środek
rotateX(mouseY*PI/300); //i obracamy go wokół osi X
rotateZ(mouseX*PI/300); //i osi Z
noFill(); //bez wypełniania
stroke(250,160); //rysujemy białym, lekko przezroczystym kolorem
Współrzędne punktów będą teraz trochę inne, a nasza krzywa będzie przypominać odwróconą literę ‘U’. Narysujemy ją 120 razy, przesuwając ją stopniowo (użyjemy znowu pętli FOR). Zauważ, że zamieniliśmy współrzędną Y ze współrzędną Z (gdzie współrzędna Y przesuwa się od -60 do 60).
for (int i=-60;i<60;i++)
{
px[0] = -100; py[0] = -50;
px[1] = -80; py[1] = 150;
px[2] = 80; py[2] = 150;
px[3] = 100; py[3] = -50;
bezier(px[0], i*2, py[0], //współrzędne pierwszego punktu (początku krzywej)
px[1 ], i*2, py[1], //współrzędne drugiego punktu
px[2], i*2, py[2], // trzeciego
px[3], i*2, py[3]); //i czwartego (koniec)
}
}
Po uruchomieniu programu, widzimy naszą pierwszą prawdziwie trójwymiarową powierzchnię :
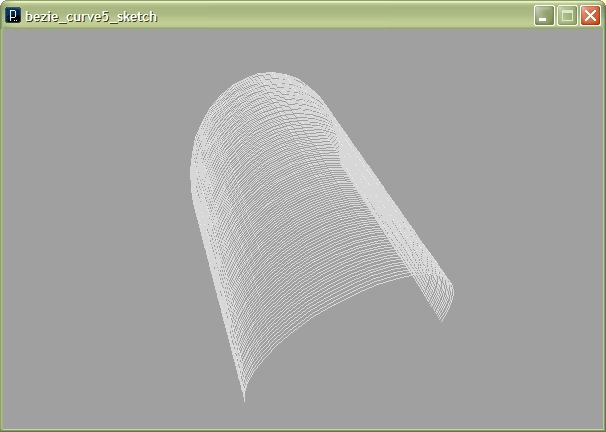
W tym momencie nasz ‘dach’ jest poprostu zwyczajną powierzchnią ‘translacyjną’, czyli powstałą poprzez translację (przesunięcie) profilu w przestrzeni. Prawdziwa zabawa zacznie się jednak dopiero, gdy zaczniemy modulować profil podczas przesuwania. Jak to zrobić ? Wystarczy przy każdym przebiegu pętli zmienić lekko współrzędne punktów kontrolnych. Dobrze jest użyć do tego funkcji Sinus lub Cosinus, ponieważ łatwo nią sterować za pomocą amplitudy i okresu. Na przykład jeśli w naszej pętli zmienna i przechodzi od wartości -60 do 60, to dodając do którejś współrzędnej wyrażenie sin(i/60 * PI) * 50 , wartość wyrażenia przejdzie płynnie od sin(-PI)*50 do sin(PI)*50, czyli od -50 do 50, oczywiście płynnym ruchem, jak na sinusoidzie.
Dodając kilka takich kombinacji można uzyskać poniższy efekt :
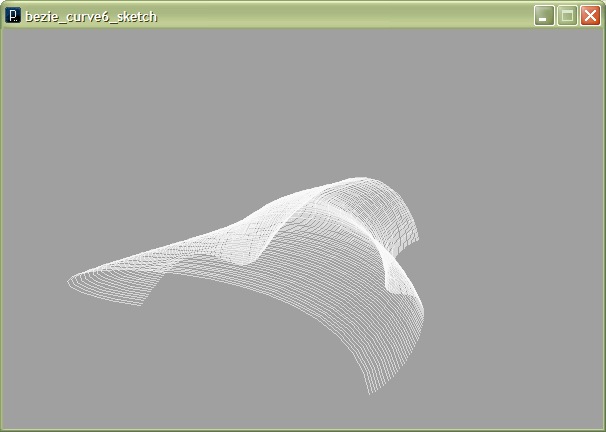
Jesteś elektrykiem, spawaczem, hydraulikiem, monterem? Sprawdź – oferty pracy za granicą.
A kod generujący krzywiznę wygląda tak :
for (int i=-60;i<60;i++)
{
px[0] = -100; py[0] = -50+sin(i*PI/60.0)*25;
px[1] = -80+sin(i*PI/45.0)*50; py[1] = 50;
px[2] = 80; py[2] = 50;
px[3] = 100+sin(i*PI/60.0)*25; py[3] = -50+sin(i*PI/40.0)*15;
bezier(px[0], i*2, py[0],
px[1], i*2+sin(i*PI/120.0)*150, py[1],
px[2], i*2, py[2],
px[3], i*2, py[3]);
}
for (int i=-60;i<60;i++)
{
px[0] = -100; py[0] = -50+sin(i*PI/60.0)*25;
px[1] = -80+sin(i*PI/45.0)*50; py[1] = 50;
px[2] = 80; py[2] = 50;
px[3] = 100+sin(i*PI/60.0)*25; py[3] = -50+sin(i*PI/40.0)*15;
bezier(px[0], i*2, py[0],
px[1 ], i*2+sin(i*PI/120.0)*150, py[1],
px[2], i*2, py[2],
px[3], i*2, py[3]);
}
Oczywiście jest to arbitralna zabawa liczbami i wyrażeniami matematycznymi, więc można dodawać i odejmować różne części wyrażeń, żeby uzyskać podobny, lub zupełnie inny efekt (np pionową fasadę zamiast poziomego dachu) – ale to już zależy od inwencji designera.
Aby zapisać tak wygenerowany ‘dach’ musimy użyć biblioteki do eksportowania geometrii do plików DXF. Tak samo jak w poprzednim odcinku, zadeklarujemy użycie tej biblioteki na samym początku programu poprzez dodanie linii
import processing.dxf.*;
Aby rozpocząć ‘łapanie’ geometrii przeznaczonej do zapisania na dysku, dodajemy linię
beginRaw(DXF, “dach.dxf”);
zaraz po linii
void draw()
{
a na samym końcu programu dodajemy endRaw(); (tuż przed nawiasem kończącym program)
}
Działający w przeglądarce powyższy przykład wraz z pełnym kodem można obejrzeć tutaj (wymagana zainstalowana Java).
Geometria zostanie zapisana w pliku ‘dach.dxf’ w tym samym folderze, w którym znajduje się nasz szkic (dobrze jest go najpierw zapisać poprzez File >> Save w głównym menu).
Należy pamiętać, żeby używać funkcji beginRaw(..) i endRaw() tylko wtedy kiedy chcemy zapisać geometrię, inaczej będzie ona spowalniać niepotrzebnie nasz program. Poza tym warto zapisywać geometrię bez żadnych obrotów – najlepiej poprostu włączyć i wyłączyć program trzymając kursor myszki poza oknem, wtedy dach będzie leżał poziomo na płaszczyźnie XY. Można też zamienić linie obracające układ współrzędnych na rotateX(0); rotateZ(0); , lub zupełnie je wyłączyć/skomentować za pomocą symbolu // (początek komentarza – tekst następujący po tym symbolu jest ignorowany).
Po wyeksportowaniu geometrii do pliku, możemy otworzyć go w programie CAD i zrobić z nim co nam się żywnie podoba
